Recursion

"To understand recursion, you must first understand recursion", yes, the meme is funny, I know. Recursion is a powerful tool, but it can be difficult to understand. I've been there, and I'm here to share my journey with you.

Think of recursion like looking into a mirror that reflects into another mirror, dream inside of another dream (Inception?), It's an infinite loop, but it's not an infinite loop. It's a paradox, and it's a challenge to wrap your head around.

My initial understanding of recursion was quite limited. I knew that it involved a function calling itself, but I didn't understand how it worked. I didn't understand how the function could call itself without causing an infinite loop, and I didn't understand how the function could return a value when it hadn't finished running yet. I was stuck in a loop of confusion, and I needed to break out of it.

The important part to understand is that a recursive function must have a base case to stop the recursion. Without a base case, the function will keep calling itself forever, and the program will crash. The base case is the exit condition that stops the recursion from continuing indefinitely.

Even though I understood the concept of the base case, I still didn't understand how the function could return a value when it hadn't finished running yet. I didn't understand how the computer kept track of all the function calls and how it knew when to stop. I was missing a crucial piece of the puzzle, and I needed to find it.

Stack

The stack is a fundamental data structure that operates on the principle of Last In First Out (LIFO). It is a linear data structure that follows a particular order in which the operations are performed. The order may be LIFO (Last In First Out) or FILO (First In Last Out). The Stack data structure is an essential part of understanding how recursion works. When a function calls itself, the computer uses a stack to keep track of the function calls. Each time a function is called, the computer pushes information about the call onto the stack. When the function returns a value, the computer pops the information off the stack and uses it to continue running the program. This process continues until the stack is empty.

I will go over more in depth about the stack data structure in a future post, but for now, let's focus on how the stack helps us understand recursion.

Visualizing Recursion with the Stack

I am a visual learner, I found that drawing out the stack helped me grasp the concept more intuitively. Let's consider a simple example: calculating the factorial of a number. The factorial of a number is the product of all positive integers less than or equal to the number. For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.

Here's a simple recursive function to calculate the factorial of a number:

cpp
int factorial(int n) {
  if (n == 0) { // base case
    return 1;
  }
  return n * factorial(n - 1);
}

Now let's visualize how the stack works when we call factorial(5):

When we first call factorial(5), it will push factorial(5) onto the stack. Then, it will call factorial(4) and push that onto the stack. This process will continue until factorial(0) is called. At this point, the stack will look like this:

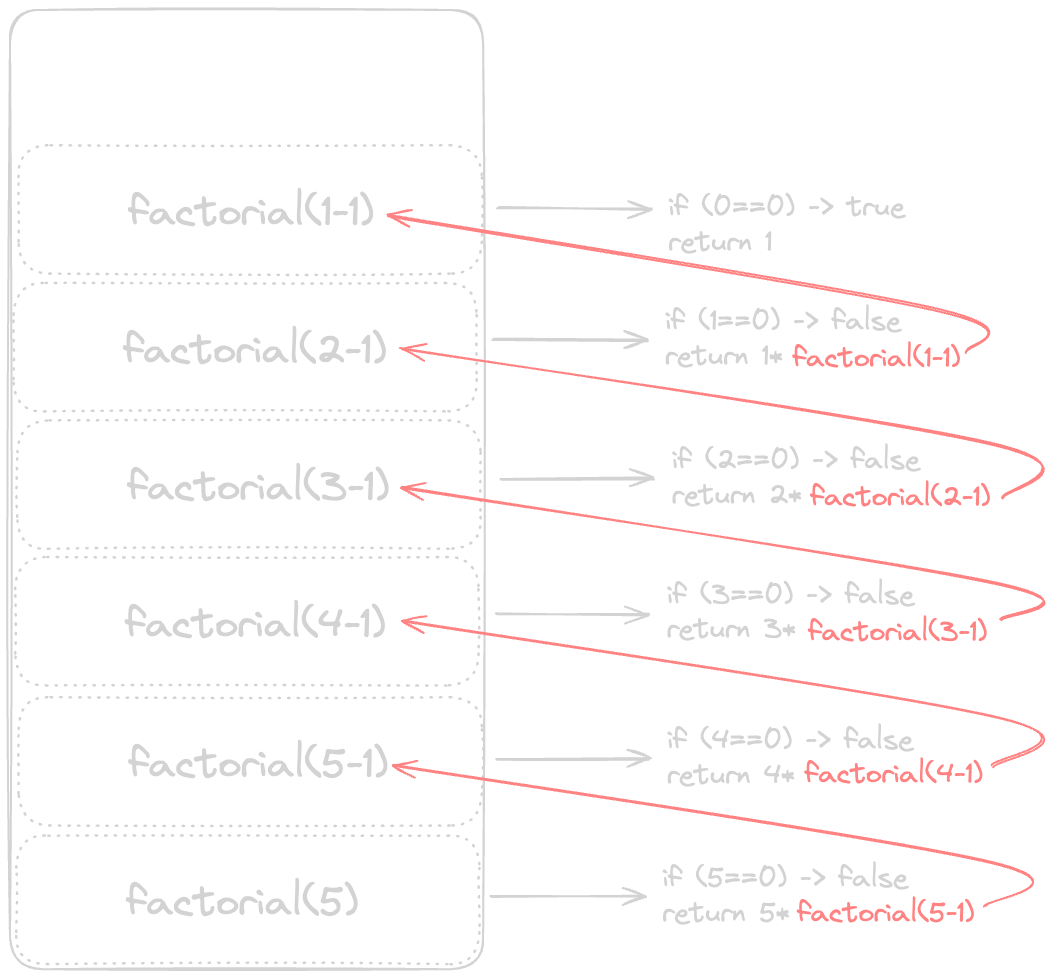
The last call to factorial(0) will return 1, and then the stack will start to unwind. Each call will return a value and pop itself off the stack. The stack will continue to unwind until it is empty.

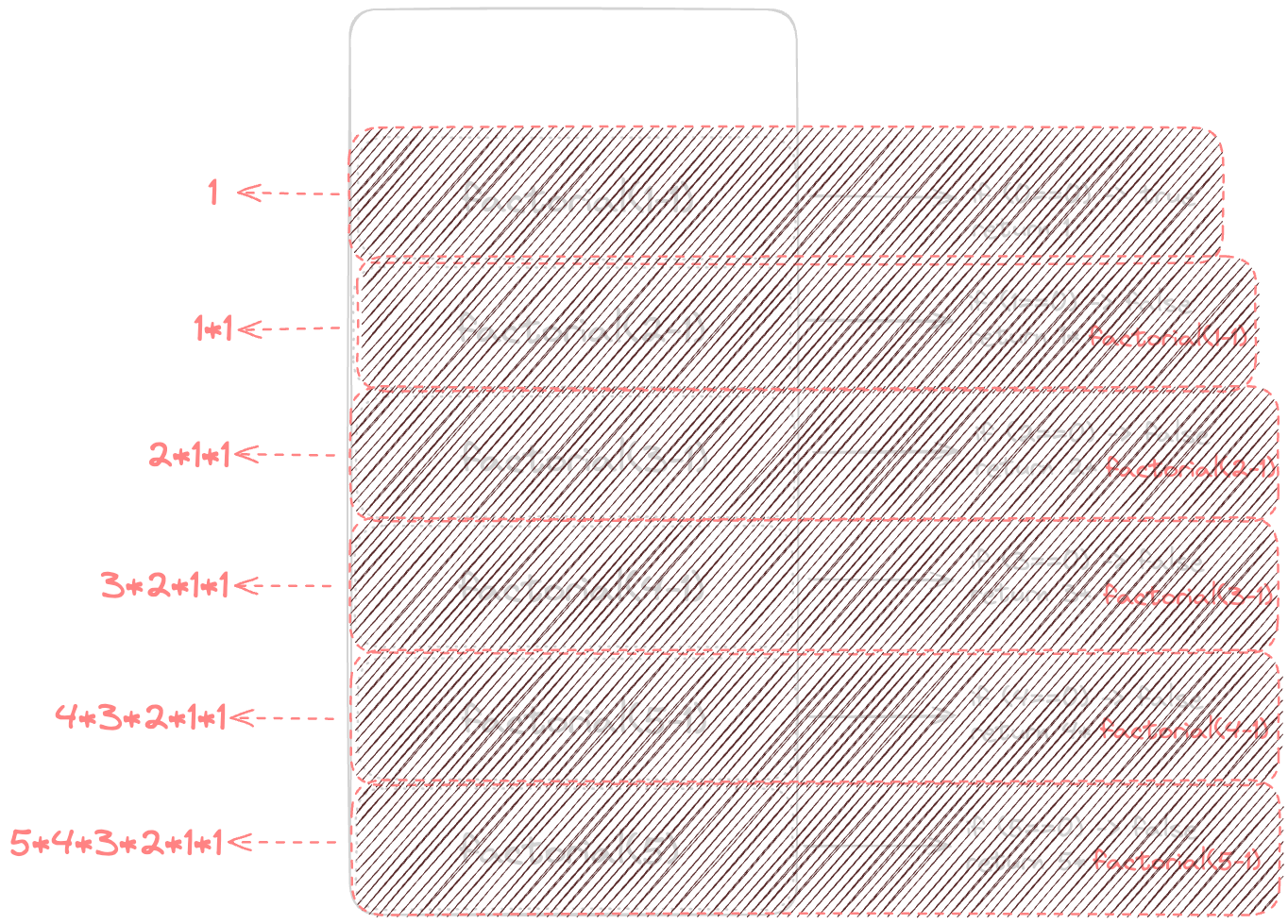
This visualization helped me understand how the stack keeps track of the function calls and how the return values are used to calculate the final result. It was a "aha" moment for me, and it opened the door to a deeper understanding of recursion.

I hope you find this post helpful in your journey to understand recursion. We all have different ways to understand complex concepts, and I found that visualizing the stack helped me grasp the concept more intuitively. If you're struggling with recursion, I encourage you to try drawing out the stack and see if it helps you too. Happy coding! 🚀